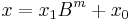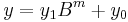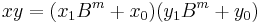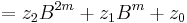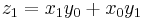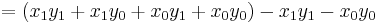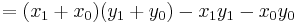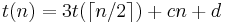Karatsuba algorithm

The Karatsuba algorithm is a fast multiplication algorithm. It was discovered by Anatolii Alexeevitch Karatsuba in 1960 and published in 1962.^[1][2][3] It reduces the multiplication of two n-digit numbers to at most 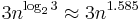single-digit multiplications in general (and exactly 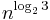when n is a power of 2). It is therefore faster than the classical algorithm, which requires n² single-digit products. If n = 2¹⁰ = 1024, in particular, the exact counts are 3¹⁰ = 59,049 and (2¹⁰)² = 1,048,576, respectively. The Toom–Cook algorithm is a faster generalization of this algorithm. For sufficiently large n, another generalization, the Schönhage–Strassen algorithm, is even faster.

The Karatsuba algorithm was the first asymptotically fast multiplication algorithm.

History

The standard procedure for multiplication of two n-digit numbers requires a number of elementary operations proportional to 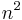, or 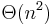in the big-O notation. In 1952, Andrey Kolmogorov conjectured that the classical algorithm was asymptotically optimal, meaning that any algorithm for that task would require 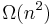elementary operations.

In 1960, Kolmogorov organized a seminar on mathematical problems in cybernetics at the Moscow State University, where he stated the 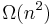conjecture and other problems in the complexity of computation. Within a week, Karatsuba, then a 23-year-old student, found an algorithm (later it was called "divide and conquer") that multiplies two n-digit numbers in 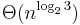elementary steps, thus disproving the conjecture. Kolmogorov was very upset about the discovery; he communicated it at the next meeting of the seminar, which was then terminated.^[2]

The method was published in 1962, in the Proceedings of the USSR Academy of Sciences.^[1] The article had been written by Kolmogorov, possibly in collaboration with Yuri Ofman, but listed "A. Karatsuba and Yu. Ofman" as the authors. Karatsuba only became aware of the paper when he received the reprints from the publisher.^[2]

Algorithm

The basic step

The basic step of Karatsuba's algorithm is a formula that allows us to compute the product of two large numbers 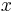and 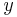using three multiplications of smaller numbers, each with about half as many digits as 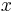or 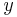, plus some additions and digit shifts.

Let 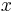and 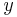be represented as 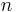-digit strings in some base 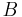. For any positive integer 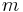less than 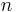, one can split the two given numbers as follows

where 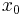and 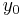are less than 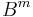. The product is then

where

These formulae require four multiplications. Karatsuba observed that 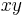can be computed in only three multiplications, at the cost of a few extra additions:

Let

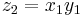
Let

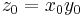
Let

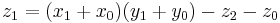
since

Example

To compute the product of 1234 and 5678, choose B = 10 and m = 2. Then

12 34 = 12 × 10² + 34

56 78 = 56 × 10² + 78

z₂ = 12 × 56 = 672

z₀ = 34 × 78 = 2652

z₁ = (12 + 34)(56 + 78) − z₂ − z₀ = 46 × 134 − 672 − 2652 = 2840

result = z₂ × 10^2×2 + z₁ × 10² + z₀ = 672 × 10000 + 2840 × 100 + 2652 = 7006652.

Recursive application

If n is four or more, the three multiplications in Karatsuba's basic step involve operands with less than n digits. Therefore, those products can be computed by recursive calls of the Karatsuba algorithm. The recursion can be applied until the numbers are so small that they can (or must) be computed directly.

In a computer with a full 32-bit by 32-bit multiplier, for example, one could choose B = 2³¹ = 2,147,483,648 or B = 10⁹ = 1,000,000,000, and store each digit as a separate 32-bit binary word. Then the sums x₁ + x₀ and y₁ + y₀ will not need an extra carry-over digit (as in carry-save adder), and the Karatsuba recursion can be applied until the numbers are only 1 digit long.

Efficiency analysis

Karatsuba's basic step works for any base B and any m, but the recursive algorithm is most efficient when m is equal to n/2, rounded up. In particular, if n is 2^k, for some integer k, and the recursion stops only when n is 1, then the number of single-digit multiplications is 3^k, which is n^c where c = log₂3.

Since one can extend any inputs with zero digits until their length is a power of two, it follows that the number of elementary multiplications, for any n, is at most .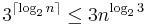

Since the additions, subtractions, and digit shifts (multiplications by powers of B) in Karatsuba's basic step take time proportional to n, their cost becomes negligible as n increases. More precisely, if t(n) denotes the total number of elementary operations that the algorithm performs when multiplying two n-digit numbers, then

for some constants c and d. For this recurrence relation, the master theorem gives the asymptotic bound .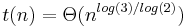

It follows that, for sufficiently large n, Karatsuba's algorithm will perform fewer shifts and single-digit additions than longhand multiplication, even though its basic step uses more additions and shifts than the straightforward formula. For small values of n, however, the extra shift and add operations may make it run slower than the longhand method. The point of positive return depends on the computer platform and context. As a rule of thumb, Karatsuba is usually faster when the multiplicands are longer than 320–640 bits.^[4]

References

• Karacuba A. A.: Berechnungen und die Kompliziertheit von Beziehungen (German). Elektron. Informationsverarb. Kybernetik, 11, 603–606 (1975).

External links

• Karatsuba's Algorithm for Polynomial Multiplication
• Weisstein, Eric W., "Karatsuba Multiplication" from MathWorld.
• Karatsuba multiplication Algorithm – Web Based Calculator (GPL)
• Bernstein, D. J., "Multidigit multiplication for mathematicians". Covers Karatsuba and many other multiplication algorithms.
• Karatsuba Multiplication on Fast Algorithms and the FEE
• Karatsuba using Sums of Squares Implementation